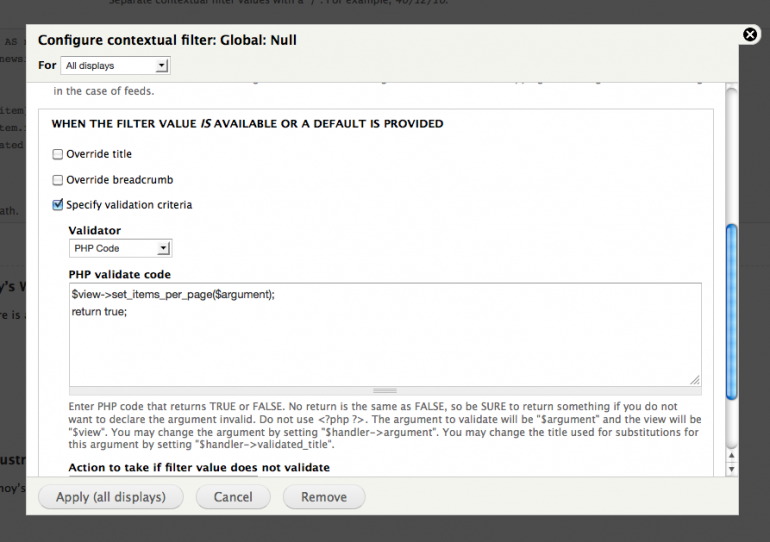
1. Create a multisite account for the site you are about to import
We set up our multisite using subdomains – this is useful for us as some of our sites there really are subdomains of the main site. If you use subfolders, some of the steps below might be different – unfortunately we havent tested them for that case.
2. Import the site
We are using the HTML Import module. You can import blog posts and pages in seperate import runs. For pages, it will keep the hierarchy.
3. Clean up superflous HTML
Sometimes there is unneeded content that appears on every page. For example our HTML sites were scraped from Plone sites, so there was lots of template cruft at the beginning and end of every post (plus the title was inside the CSS class that served as our ‘body’ class, so it ended up inside the main content too). So here’s a little php script you can modify for your own ends. Note that you will also need to download the htmLawed script and place it in the same folder as the script below.
2,
'tidy' => 1,
'elements' => $elements,
'cdata' => 1,
'comment' => 1,
'deny_attribute' => 'align'
);
mysql_select_db($dbname);
$doc = new DOMDocument();
$query = mysql_query("SELECT ID, post_date, post_title, post_name, post_content, post_type FROM " . POSTTABLE . " WHERE post_type IN ('post', 'page') AND post_status = 'publish'");
while($post = mysql_fetch_object($query)) {
if(TESTINGSINGLE == false || $post->ID == TESTID) {
print "\n\n" . '**opening ' . $post->ID . ' - name: ' . $post->post_name . "\n";
}
$oldpost = $post->post_content;
$doc->loadHTML($oldpost);
$newtabledom = new DOMDocument;
$xpath = new DOMXPath($doc);
$newtabledom = $doc;
$pagepath = new DOMXPath($newtabledom);
// Remove content inside certain classes inside page
// The below elements are leftover elements from Plone
// See XPath documentation for more details of how to make queries
$toremove= $pagepath->query("//h1[@class='documentFirstHeading'] | //p[@class='documentDescription'] | //div[@class='documentDescription'] | //div[@class='documentByLine'] | //div[@class='documentActions'] | //div[@id='relatedItems'] | //div[@class='discussion'] | //a[@id='documentContent'] | //a[@class='link-parent']");
foreach ($toremove as $entry) {
$entry->parentNode->removeChild($entry);
}
// We try and change classes of images to use the WordPress floated classes
// The script detects classes (or parent div classes) that have the words
// left right or center and renames them
$imgtags = $doc->getElementsByTagName('img');
foreach($imgtags as $child) {
$linkclass = $child->attributes->getNamedItem('class')->nodeValue;
$alignclass = $child->attributes->getNamedItem('align')->nodeValue;
$linkfile = $child->attributes->getNamedItem('src')->nodeValue;
if(strpos($linkclass, 'left') !== false || strpos($alignclass, 'left') !== false) {
$child->setAttribute( 'class' , 'alignleft' );
}
else if (strpos($linkclass, 'right') !== false || strpos($alignclass, 'right') !== false) {
$child->setAttribute( 'class' , 'alignright' );
}
else if (strpos($linkclass, 'centre') !== false || strpos($linkclass, 'center') !== false
|| strpos($alignclass, 'centre') !== false || strpos($alignclass, 'center') !==false ) {
$imageinfo = @getimagesize(SITEROOT . $linkfile);
$child->setAttribute( 'class' , 'aligncenter' );
}
else {
// get parent
$parent = $child->parentNode;
if ($parent) {
$grandparent = $parent->parentNode;
$parentclass = $parent->attributes->getNamedItem('class')->nodeValue;
$parentalign = $parent->attributes->getNamedItem('align')->nodeValue;
$grandparentclass = $grandparent->attributes->getNamedItem('class')->nodeValue;
$grandparentalign = $grandparent->attributes->getNamedItem('align')->nodeValue;
}
else {
$parentclass = '';
$parentalign = '';
$grandparentclass = '';
$grandparentalign = '';
}
if (strpos($parentclass, 'left') !== false || strpos($parentalign, 'left') !== false) {
print "\n\n" . '** left parent ' . $linkfile . " - class: " . $parentclass . " - align: " . $parentalign. "\n";
$child->setAttribute( 'class' , 'alignleft' );
}
else if (strpos($parentclass, 'right') !== false || strpos($parentalign, 'left') !== false) {
print "\n\n" . '** right parent ' . $linkfile . " - class: " . $parentclass . " - align: " . $parentalign. "\n";
$child->setAttribute( 'class' , 'alignright' );
}
else if (strpos($parentclass, 'centre') !== false || strpos($parentclass, 'center') !== false
|| strpos($parentalign, 'centre') !== false || strpos($parentalign, 'center') !== false) {
print "\n\n" . '** centred parent ' . $linkfile . " - class: " . $parentclass . " - align: " . $parentalign. "\n";
$imageinfo = @getimagesize($linkfile);
$child->setAttribute( 'class' , 'aligncenter' );
}
else if (strpos($grandparentclass, 'left') !== false || strpos($grandparentalign, 'left') !== false) {
print "\n\n" . '** left grandparent ' . $linkfile . " - class: " . $grandparentclass . " - align: " . $grandparentalign. "\n";
$child->setAttribute( 'class' , 'alignleft' );
}
else if (strpos($grandparentclass, 'right') !== false || strpos($grandparentalign, 'left') !== false) {
print "\n\n" . '** right grandparent ' . $linkfile . " - class: " . $grandparentclass . " - align: " . $grandparentalign. "\n";
$child->setAttribute( 'class' , 'alignright' );
}
else if (strpos($grandparentclass, 'centre') !== false || strpos($grandparentclass, 'center') !== false
|| strpos($grandparentalign, 'centre') !== false || strpos($grandparentalign, 'center') !== false) {
print "\n\n" . '** centred grandparent ' . $linkfile . " - class: " . $grandparentclass . " - align: " . $grandparentalign. "\n";
$imageinfo = @getimagesize($linkfile);
$child->setAttribute( 'class' , 'aligncenter' );
}
}
}
// Replace underscores with dashes inside relative links
// we are excluding ../ links for now - too complicated
$atags = $doc->getElementsByTagName('a');
foreach($atags as $child) {
$linkhref = $child->attributes->getNamedItem('href')->nodeValue;
if (!(substr($linkhref, 0, 4) == 'http' || substr($linkhref, 0, 1) == '/' || substr($linkhref, 0, 3) == '../')) {
$parent = mysql_fetch_object(mysql_query("SELECT post_name FROM " . POSTTABLE . " WHERE post_parent = " . $post->post_parent));
// print "\n\n" . 'parent name: ' . $parent->post_name . "\n";
if(strpos($linkhref, '_') !== FALSE && (strpos($post->post_name, '-') !== FALSE || strpos($parent->post_name, '-') !== FALSE) ) {
print "\n\n" . 'link: ' . $linkhref . "\n";
$linkhref = str_replace('_', '-', $linkhref);
$linkhref = preg_replace('/--+/', '-', $linkhref);
print "\n\n" . 'changed internal link: ' . $linkhref . "\n";
$child->setAttribute( 'href' , $linkhref);
}
}
}
// Output HTML from query documents
$newtablehtml = $newtabledom->saveHTML();
// Text rewriting
// This can be modified to your needs
$newtablehtml = str_replace('[...]', '', $newtablehtml);
$newtablehtml = str_replace('/index.html"', '"', $newtablehtml);
$newtablehtml = str_replace('/"', '"', $newtablehtml);
$newtablehtml = str_replace('https://my.', 'http://www.', $newtablehtml);
// Sometimes there are encoding issues which need dealing with
$newtablehtml = str_replace('Â ', '', $newtablehtml);
$newtablehtml = str_replace('Â', '', $newtablehtml);
$newtablehtml = str_replace('„', '', $newtablehtml);
$newtablehtml = str_replace('’', "'", $newtablehtml);
$newtablehtml = str_replace("‘", "'", $newtablehtml);
$newtablehtml = str_replace("’", "'", $newtablehtml);
$newtablehtml = str_replace("“", "'", $newtablehtml);
$newtablehtml = str_replace("”", "'", $newtablehtml);
$newtablehtml = str_replace("–", " - ", $newtablehtml);
$newtablehtml = str_replace("—", " - ", $newtablehtml);
$newtablehtml = str_replace("’", "'", $newtablehtml);
$newtablehtml = str_replace("“", "", $newtablehtml);
$newtablehtml = str_replace("”", "", $newtablehtml);
// Sometimes the old page still contains html doctype
// inside the content tag
if (strpos($newtablehtml, '') !== 0) {
$newtablehtml = str_replace('', '', $newtablehtml);
}
// Remove empty paragraphs
$newtablehtml = preg_replace("#]*>(\s| ?)*#", '', $newtablehtml);
// Now run htmLawed to clean up
$newtablehtml = htmLawed($newtablehtml, $config);
// Normalise post titles in all caps
if (strtoupper($post->post_title) == $post->post_title) {
$post->post_title = ucwords(strtolower($post->post_title));
}
if(strlen($newtablehtml) > 30) {
// Post name exists - save new post content only
if(strlen(trim($post->post_name)) > 0) {
if(TESTINGSINGLE == false || $post->ID == TESTID) {
$query2 = "UPDATE " . POSTTABLE . " SET post_content = '" . mysql_real_escape_string($newtablehtml) . "', post_title = '" . $post->post_title . "' WHERE ID = ". $post->ID;
mysql_query($query2);
}
}
// Need to generate post content from title
else {
$postname = strtolower(sanitize_file_name($post->post_title));
if(TESTINGSINGLE == false || $post->ID == TESTID) {
$query2 = "UPDATE " . POSTTABLE . " SET post_content = '" . mysql_real_escape_string($newtablehtml) . "', post_name ='" . mysql_real_escape_string($postname) . "',post_title = '" . $post->post_title . "' WHERE ID = ". $post->ID;
mysql_query($query2);
}
}
} else {
// Delete posts with v little or no content
$query3 = mysql_query("SELECT ID FROM " . POSTTABLE . " WHERE post_type IN ('post', 'page') AND post_status = 'publish' AND post_parent = " . $post->ID);
if(!mysql_fetch_object($query3)) {
if(TESTINGSINGLE == false || $post->ID == TESTID) {
mysql_query("DELETE FROM " . POSTTABLE . " WHERE ID = ". $post->ID);
}
}
}
}
// Taken from the WP function
function sanitize_file_name( $filename ) {
$filename_raw = $filename;
$special_chars = array("?", "[", "]", "/", "\\", "=", "<", ">", ":", ";", ",", "'", "\"", "&", "$", "#", "*", "(", ")", "|", "~", "`", "!", "{", "}", "–", "—","—", chr(0));
$filename = str_replace($special_chars, '', $filename);
$filename = preg_replace('/[\s-]+/', '-', $filename);
$filename = trim($filename, '.-_');
$entities = array("%e2", "%80", "%9c", "%9d", "%94", "%a0". "%93", "%99");
$filename = str_replace($entities, '', $filename);
$unique = 0;
$i = 0;
while (!$unique) {
$query = mysql_query("SELECT post_name FROM " . POSTTABLE . " WHERE post_name IN ('post', 'page') AND post_name = '" . $filename . "'");
if(mysql_fetch_object($query)) {
print('***not unique - ' . $filename);
$filename = $filename . '-' . $i;
$i = $i + 1;
}
else { $unique = 1; }
}
return $filename;
}
?>
4. Create redirections from one site to another
The also generates a very nice .htaccess file we can use as the basis for our redirects. Unfortunately we can’t use this directly in the .htaccess file for wordpress multisites, as the same htaccess file is used across all sites. Fortunately we can use the Redirection module, which lets WordPress handle the redirections instead of Apache.
For static sites, we often need to cater for the case where the URL ends in / as well as /index.html. So we need to rewrite our redirects a little – heres a little shell script you can run. Copy the generated .htaccess file to your desktop and run
# specify your original domain here - ie the one that occurs first in the .htaccess rule
DOMAIN = http://www.domain.com
# Replace tabs with spaces - much easier to deal with
expand -t1 htaccess > htaccess1
# this replaces your domain with ^/ - makes it much easier to target remaining
sed 's-$DOMAIN/-^/-g' htaccess2 > htaccess3
# Use RedirectMatch
sed 's/Redirect/RedirectMatch 301/g' htaccess3 > htaccess4
# We wont use the mod_rewrite way as Redirect doesnt handle that
sed 's/[R=301,NC,L]//g' htaccess4 > htaccess5
# This tacks on a regex that will handle / and index.html at the end of a URL
# note: this is for the case where your static URLS in .htaccess dont end in
# either / or /index.html
sed 's- http://-(:?/index.html|/)?$ http://-g' htaccess5 > htaccess_new
# comment the above line and uncomment one of these if your static URLs
# end in / (1st one) or /index.html (2nd one)
# sed 's-/ http://-(:?/index.html|/)?$ http://-g' htaccess5 > htaccess_new
# sed 's-/index.html-(:?/index.html|/)?$-g' htaccess5 > htaccess_new
Test it out on one line, and then see if it works.